Susceptible, Infectious, Recovered

On​ 12 March, Boris Johnson confirmed that the most stringent measures other countries had introduced to control the spread of Covid-19 would not be applied in the UK. Flanked by the government’s chief scientific officer and its chief medical officer, he stressed that this decision was in accordance with the best scientific evidence. This included mathematical modelling of the epidemic by two of the world’s leading teams, one based at the London School of Hygiene and Tropical Medicine and the other at Imperial College London. Other countries had locked down their economies in an effort to suppress the pandemic, but in the UK the strategy, supposedly supported by the evidence of these modellers, was instead to delay the disease and thus mitigate its consequences. I was surprised: at UCL we had already begun to move teaching online in anticipation of the closure of schools and university campuses. Companies had begun to shift staff to working from home, sporting events were being cancelled, NHS trusts were postponing routine surgery.

A simple mathematical model of the course of an epidemic.

Only a few days later, however, government policy began to change. Schools were told to close on 18 March; two days later pubs and restaurants were shut; and on 23 March the government announced a lockdown. Given the value of early intervention in dealing with an exponentially growing epidemic, persisting with the mitigation strategy for as long as the government did looks like a hugely consequential mistake. Journalists have begun to question whether the government really did at all times follow the scientific advice, based on mathematical modelling, it was given.

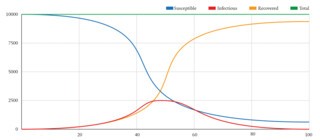
You can build a simple mathematical model of an epidemic in a spreadsheet, using three columns to represent the Susceptible, the Infectious and the Recovered and calculating daily totals to show how an imaginary population is affected. The SIR model has two mathematical formulae controlling the flow from Susceptible to Infectious and from Infectious to Recovered. These formulae tell us how many people to subtract each day from the Susceptible population and add to the Infectious, and how many to subtract from the Infectious and add to the Recovered. The number of people moved out of the Susceptible group is calculated from the average number of contacts each individual has, the likelihood that a contact is with an infectious person, and the likelihood that such contacts will lead to infection. The number moved from Infectious to Recovered is simply the number of infectious individuals multiplied by the average rate of recovery.

I generated the graph shown here from a spreadsheet set up in the way I have described.* I took a population of 10,000 and started with 9999 susceptible people and one infectious person. I set the number of contacts per person per day at 13 and the probability of an instance of contact resulting in disease transmission at 3 per cent. I set the rate of recovery so that 15 per cent of the infectious population recover each day. It shows the epidemic peaking at day 45, at which point 2068 people are infectious. By day 100, it is almost over. Not everyone has been affected – there are still 854 Susceptibles – but since day 45 the likelihood that any of their contacts will be in the Infectious group has been diminishing and is now getting close to zero. To put it another way, because the 9139 Recovered are no longer susceptible, their immunity is enough to guarantee the immunity of the herd.

This model has four parameters: 13, the average number of contacts per person per day; 3 per cent, the probability that a contact will lead to transmission; 15 per cent, the rate at which people recover; and 10,000, the size of the population. The product of the first two numbers determines how fast the population flows into the Infectious group, while the third number determines how fast it moves from Infectious to Recovered. Dividing the product of the first two numbers by the third gives the expected number of transmissions from a single case, also known as R₀ or the basic reproduction rate. In this example it is 13 x 3 ÷ 15, which is 2.6: in other words, when everyone is susceptible, each infectious person will infect, on average, 2.6 others, leading to an exponential increase in infections until the supply of non-infectious people begins to run out. You can play with the numbers and see how the quickly the epidemic spikes when R₀ is 3 or 4, and how the combination of parameters affects the level of infection needed before the herd attains immunity: the more contagious a disease the higher the percentage of people who need to be immune to it.

The teams that have been advising the government have now published accounts of their models. The one from the London School of Hygiene and Tropical Medicine (LSHTM) is superficially similar to mine. Susceptible people pass through a latent phase between becoming infected and being infectious, and then either have a mild, or subclinical, version of the disease, or a more serious illness with both a preclinical phase and a clinical phase requiring a stay in hospital. It is assumed that the mild cases are only half as infectious as the more severe cases.

Only one of the parameters in my model – the average number of contacts per person per day – is a fact about human behaviour. This is the parameter that can be manipulated when we attempt to alter the course of a pandemic. In the LSHTM model a separate value for the average number of contacts was calculated for every five-year age band in each of the 186 county-level administrative units in England, Wales, Scotland and Northern Ireland. To do this, demographic data on the proportion of people in each age group in each county was combined with data from an EU-funded study from 2008 (which seems to have been carried out in anticipation of a need for this kind of modelling) that surveyed 7290 people of different ages and asked them about the number of people they typically encountered at home, at work, at school or elsewhere. In my model the transitions between phases were determined by applying an average figure to everyone in each group at a particular time. In the LSHTM model the probability of each individual moving from one phase to the next at a given time was drawn from a range of values taken from early analyses of data from Wuhan. The length of time between onset and death, for example, is modelled using data that a Japanese team collated on 44 patients for whom those dates were reported either on Chinese government websites or in news stories.

The rate at which the number of cases increases is determined by R₀, and since the increase in Covid-19 cases is exponential, the accuracy with which this figure can be estimated is of crucial importance. The LSHTM team found 11 published estimates of R₀ for Covid-19, which averaged at 2.68 with a standard deviation of 0.57. Equally important is the estimate of the proportion of infected people who will die. Epidemiologists use two different measures for this, the Case Fatality Rate (CFR), the number of deaths divided by the number of confirmed cases, and the Infection Fatality Rate (IFR), the number of deaths divided by the total number of cases, including those that aren’t confirmed. The LSHTM team first calculated age-specific CFRs suggested by Chinese reports of cases and fatalities, and then adjusted these estimates using data from the 3711 passengers on the Diamond Princess cruise ship, who, almost as if they were subjects in a research trial conducted for this purpose, had been repeatedly tested for the disease whether or not they had symptoms.

The model predicted that, if nothing was done to mitigate the effects of the epidemic in the UK, 85 per cent of the population would be infected, there would be 24 million clinical cases and 370,000 deaths. At its peak, 220,000 ICU beds would be required. In February this year the number of adult ICU beds open in England was 4122. The effects of different policies – school closures, social distancing, shielding of the elderly and self-isolation of symptomatic individuals – and of combinations of them were simulated by adjusting the average number of contacts. The most effective single strategy, shielding the elderly, still resulted in 220,000 deaths and a need for 120,000 ICU beds, as well as 230,000 other hospital beds. There are about 100,000 general and acute NHS hospital beds currently available in England.

The LSHTM team also modelled the impact of more aggressive strategies, such as the use of repeated lockdowns, triggered when the number of ICU beds occupied by Covid-19 patients reaches a particular number. If the threshold was set at a thousand ICU beds, the number of cases could be kept to four million and the number of deaths to 51,000. The downside is that 73 per cent of the time between now and December 2021 would be spent in lockdown, by which point only 11 million people would have been infected and, unless a vaccine had been found, the epidemic would be far from over.

The details of this work were published in a report dated 1 April. The authors note that a worst-case scenario for the path of the epidemic in a single city was presented to the government on 26 February, and the modelling of the impact of mitigation strategies at a national level on 2 March, then in an expanded form on 8 March. On the 11 March the team presented its analyses of the potential impact of repeated periods of lockdown, which were then updated after the change in government thinking. The LSHTM team state that, although the available data and thus the modelling changed during February and March, ‘our overall conclusions about the relative effectiveness of different strategies for reducing the burden of Covid-19 in the UK are the same as those presented to decision-makers in real time.’ The Sunday Times report of 19 April on the government’s response to the pandemic gives the impression that the LSHTM team warned the government on 26 February that a lockdown was necessary. Dr Nick Davies, who carried out the work, told me that there is no justification for this claim.

The Imperial model was originally devised to assess the effectiveness of possible responses to an epidemic of avian flu in Thailand, and the most detailed published account of it comes in the ‘supplementary information’ to that paper. In this model, a population of individuals is constructed, mirroring the one to be studied, and each individual is ascribed a risk of infection. The individuals are defined by three parameters: their age, their household and their ‘place’ – which can be at school or at work. Each of them can be at home, in their ‘place’ or moving around in the community. Households, school classes and workplaces are generated so that their sizes and age distributions reflect those in the relevant country, in this case the UK.

Like the LSHTM team, the Imperial group’s understanding of the way the disease would behave and would be experienced was based initially on data from China. The variation in the length of time between the onset of symptoms and eventual death was estimated from just 24 patients in Wuhan, and the profile of the length of time it took patients to recover was estimated from 165 patients. Age-stratified mortality rates were calculated from a much larger group: by 9 March the team had data on 1072 deaths and 44,672 confirmed cases in mainland China. The team knew the age breakdown only for patients who had died, so calculated age-stratified mortality rates by making assumptions about the way cases were distributed, one of which was that the disease had a ‘uniform attack rate’. Although the team knew that older people developed more severe symptoms, they assumed that all age groups were equally likely to become infected and that the difference lay in the way the virus affected different age groups. The prevalence of asymptomatic cases in the wider population was estimated, as it had been in the LSHTM model, by using the data about passengers on the Diamond Princess, but the Imperial team added data from another group that had been exhaustively tested whether or not they were symptomatic: passengers on six flights repatriating foreign nationals who had been in Wuhan.

The results of modelling carried out by the Imper­ial team showing the results of different mitigation strategies on demand for critical care beds.

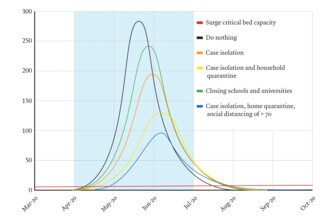
A 16 March report from the Imperial team used its model to compare a range of options designed to mitigate the effects of the epidemic in the UK, and an alternative strategy designed to suppress it completely. The options for mitigation were case isolation, voluntary home quarantine, social distancing of the over-seventies, social distancing for everyone, and school and university closures. Each was modelled by adjusting the parameters determining the number of contacts a person had in their household, at their workplace or school, and in the community. The team estimated that if nothing was done 550,000 people would die, and that a combination of all the contemplated mitigation strategies would do no better than halve that total. The only alternative approach was to apply a combination of strategies to suppress the epidemic, bringing R₀ down below one. The problem with this, as the report highlighted and as the LSHTM’s modelling had also shown, is that the virus doesn’t go away. The number in the Infectious column shrinks, but not to zero, and since the majority of the population remains in the Susceptible group, once controls are relaxed the epidemic will start to grow again. Like the LSHTM, the Imperial team suggested that the least bad option was a repeated relaxation and tightening of controls, using demand for ICU beds as a trigger, until a vaccine is found.

Given that government policy changed to suppression around 16 March, its claim to have been guided throughout by the science implies that there was a change in the available evidence at this point. Neither team had initially considered suppression realistic. ‘Prior to this epidemic, I don’t think suppression of a respiratory disease was really an option in the modern world (even though US cities tried it in 1918),’ Neil Ferguson, who leads the team at Imperial, wrote to me. ‘China showed it was possible, though it was late February before it was clear it had worked. That and the Italian experience changed the debate in late February, early March. We had modelled a wide range of policy options from February onwards, ranging from lockdown-type measures to mitigation strategies with more of a focus on shielding elderly groups. The gradual firming up on the expected numbers of deaths and ICU demand was the principal driver in shifting the debate (here and across the world) towards suppression strategies.’ Things changed quickly. The estimates of Infection Fatality Rates in the Imperial team’s 16 March report are worse than those published by the same team only a week earlier. In a report dated 9 March, the proportion of cases requiring hospitalisation in people aged between 70 and 79 was estimated at 16.6 per cent, and the Infection Fatality Rate at 4.3 per cent. By 16 March these estimates had been revised upwards, partly because the assumption of a ‘uniform attack rate’ had been dropped in favour of modelling the spread of disease according to age. The new figures for people between 70 and 79 were 24.3 per cent and 5.1 per cent respectively.

The modellers seem to have struggled to map the Chinese experience onto the British health system in a way that allowed a classification of severity they could use to predict demand for ventilators and ICU beds. The Imperial team’s earlier reports have the detailed methodological supplements characteristic of scientific work, but sections of the 16 March report have a back-of-the-envelope quality. For all the sophistication of their methods, some numbers can only be guessed. A personal communication from a clinician who had experience of the epidemic in China, Italy and, in its early stages, the UK, is cited as evidence that 30 per cent of those who are hospitalised will require critical care; bed demand is ‘assumed’ to be eight days if critical care is not required, 16 days if it is. You get a sense that a stark reality is being newly confronted. The 16 March report makes clear that the conclusion that suppression is the only available option ‘has only been reached in the last few days, with the refinement of estimates of likely ICU demand due to Covid-19 based on experience in Italy and the UK (previous planning estimates assumed half the demand now estimated) and with the NHS providing increasing certainty around the limits of hospital surge capacity’.

‘It is not at all certain that suppression will succeed long-term,’ the report concludes. ‘No public health intervention with such disruptive effects on society has been previously attempted for such a long duration of time. How populations and societies will respond remains unclear.’ Both teams showed that the death rates associated with mitigation were appallingly high, but neither presented suppression as an attractive option. The government is now keen to claim it was never prepared to tolerate high levels of infection in order to achieve herd immunity, but while it was defending the mitigation strategy it was prepared to argue that the problem with suppression was that it couldn’t go on for ever and when the lockdown was lifted, the epidemic would return. That remains a strong possibility. Either way, it must have been clear long before suppression succeeded mitigation that the requirements for Personal Protective Equipment, PCR testing, ventilators and ICU beds would hugely exceed the available supply. Ferguson said that Imperial stopped modelling strategies based on widespread testing after 28 January, when Public Health England told them there wasn’t the capacity to carry it out.

The​ argument between mitigation and suppression now seems to have been settled in favour of the latter. But when the lockdown ends, a calculation will still have to be made about the relative merits of unappealing alternatives. The poor public understanding of mortality rates won’t make this any easier. The situation isn’t helped by the fact that two very different numbers are reported: daily totals of confirmed cases who died in hospital and weekly totals of later registrations, including many, perhaps 18 per cent of the total, who died outside hospital – in care homes, for example. The reporting of the epidemic also fails to place deaths from the virus in the context of normal mortality rates. When you read the daily updates of the number of hospital deaths, you aren’t reminded that last year, in England, an average of 1360 people died every day, a total of 496,354 for the year. In London right now, the death rate is way above normal, but for the UK as a whole the number of deaths in March 2020 was lower than in the same month last year.

The deaths must also be contextualised in another way. Of the 3912 people in the UK who died in March of Covid-19, 91 per cent had at least one pre-existing condition; on average they had 2.7. The numbers may change, but at that point the background risk of mortality for patients in their seventies with this number of pre-existing conditions was greater than the risk associated with Covid-19: the latter is estimated by the Imperial team as 5.1 per cent, while the background risk over one year rises from 5.9 per cent in a man aged between 70 and 74 with two pre-existing conditions to 15 per cent for a man aged between 75 and 79 with three. In other words, many of those who died would have died anyway, though they would no doubt have had ‘better’ deaths, and those deaths would have been spread out over a longer period. This isn’t to say that these deaths don’t matter, or to forget that although there are proportionally many fewer healthy young people in the statistics, they too have died in numbers that in normal times would be shocking.

One way to assess the impact of the epidemic is to focus not on the number recorded as dying of Covid-19, but on the way the epidemic has altered the total number of deaths. This means removing from consideration those for whom Covid-19 altered the manner, but not the timing, of death. It means including those who died as a result of this crisis, but who are not recorded as dying of Covid-19: those, for example, killed by heart attacks or strokes because they struggled to get care during the epidemic, or felt they shouldn’t ask for it. It would also mean including Covid-19 deaths where the attending doctor wasn’t sufficiently confident of the diagnosis – often because the patient hadn’t been tested – to record it on the death certificate. Future historians may also want to include deaths attributable to the economic consequences of the lockdown, a figure that could well dwarf all the others. People will vary enormously in their reaction to these issues. A marginal reduction in the length of a long life will seem much less important to someone for whom the end is very far away, while the economic consequences of continuing the lockdown will seem less significant to someone who has a guaranteed income from their pension.

The burden of the pandemic has so far fallen mainly on countries in South-East Asia, which coped with it relatively well, and Europe and North America, where the results have been more variable. Its spread will be global. We don’t have the data for many low and middle-income countries that would allow us to run detailed simulations of the kind I have described here. The Imperial team used a simple SIR model, adding survey data, where it exists, to estimate age-specific contact rates, which were then combined with demographic data and the Infection Fatality Rate estimates from China. The results suggest that, if nothing is done, the pandemic will lead to seven billion infections and forty million deaths worldwide. These figures could, in theory, be halved if various mitigation strategies were deployed, but healthcare systems everywhere would still be overwhelmed. The conclusion for the world is the same as it was for the UK. The only option is suppression, and its consequences, economic and social, are unknown.