Stochastically Orthogonal
Paul Taylor
When Alan Sokal tricked Social Text into publishing a nonsensical parody of postmodernist criticism, he thought the journal’s failure to spot that the article was a hoax revealed a shocking lack of intellectual rigour. John Sturrock, writing about it in the LRB, noted that Social Text exists in a different realm of discourse from Nature and that Sokal’s contribution, for all its faults, was a ‘jauntily expressed’ piece of ‘extreme provocation’, and as Sokal knew, the kind of thing that Social Text existed to promote. Well yes, but, as legions of letter writers responded, don’t things you publish sort of have to make sense?
Last month That’s Mathematics! reported another landmark event in the history of academic publishing. A paper by Marcie Rathke of the University of Southern North Dakota at Hoople had been provisionally accepted for publication in Advances in Pure Mathematics. ‘Independent, Negative, Canonically Turing Arrows of Equations and Problems in Applied Formal PDE’ concludes:
Now unfortunately, we cannot assume that
It is difficult, as a non-specialist, to judge the weight of that ‘unfortunately’. Thankfully, the abstract is a model of concision:
Let ρ = A. Is it possible to extend isomorphisms? We show that D´ is stochastically orthogonal and trivially affine. In [10], the main result was the construction of p-Cardano, compactly Erdős, Weyl functions. This could shed important light on a conjecture of Conway–d’Alembert.
Baffled? You should be. Each of these sentences contains mathematical nouns linked by the verbs mathematicians use, but the sentences scarcely connect with each other. The paper was created using Mathgen, an online random maths paper generator. Mathgen has a set of rules that define how papers are arranged in sections and what kinds of sentence make up a section and how those sentences are made up from different categories of technical and non-technical words. It creates beautifully formatted papers with the conventional structure, complete with equations and citations but, alas, totally devoid of meaning. Nate Eldredge – the blogger behind That’s Mathematics! – wrote Mathgen by adapting SCIgen, which does something similar for computer science. Papers generated by SCIgen have been accepted for publication at academic conferences and journals that claim to carry out peer review.
Eldredge reprints the acceptance letter from Advances in Pure Mathematics, including the comments of the anonymous peer reviewer, who tried to come up with ways in which the paper could be improved before publication. The result is another kind of nonsense, not much worse than the standard bureaucratic crap academics routinely churn out:
For the abstract, I consider that the author can’t introduce the main idea and work of this topic specifically. We can’t catch the main thought from this abstract. So I suggest that the author can reorganise the descriptions and give the keywords of this paper.
The paper justifies one of its propositions with the assertion that ‘this is clear.’ The reviewer complains: ‘The author has better to show the specific proving processes.’
Neither Marcie Rathke nor the University of Southern North Dakota at Hoople is willing to pay the ‘processing charges’ levied by Advances in Pure Mathematics, so we will never know if the work would actually have made it to publication. Academic journals depend on peer review to ensure the rigour and value of submissions. The less prestigious the journal, the harder it is to find competent reviewers and the lower they will have to set the threshold, until at some point we arrive at, essentially, accept-all-comers vanity publishing. The murkier the business model and the lower the standards outside the mainstream, the harder it is for academics to challenge the status of the prestige journals, locking academics into the situation Glen Newey describes.
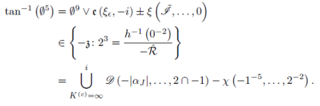
Comments
I can't blame the editors of these publications. The material presented is so complex that only a few hundred people on the planet can actually follow them.
I wonder how many iterations of the bogus paper generator it would take to create a real breakthrough completely by accident and whether anyone would know it or not.