After the Deluge

First the rainbow brought messages, later it demanded explanations. In the story of Noah it is God’s promise of an end to floods; in Greek mythology, Iris was both goddess of the rainbow and the messenger of the gods. Then, once a scientific theory was called for, it proved far from easy to come up with a satisfactory one.

Most natural historians can store their specimens: butterflies on pins, rocks in drawers, pressed plants on sheets of paper. The collector of rainbows has only words and pictures to go on. If you shine artificial light through a man-made spray you can measure refraction, reflection and the interference between incident and reflected rays precisely, but experiments do not replicate or explain everything you see in the field, which is where rainbow behaviour, like animal behaviour, must be studied. There, too, rainbows are different from most natural phenomena. Accounts of volcanic eruptions, the migration of birds and the occurrence of fossils are tested by quantitative measurement and statistics; rainbow theory is tested by comparing precisely measured angles with those that mathematical physics predicts. You quickly get into difficult stuff. For example, theories about the nature of light – is it made up of waves or corpuscles? – were challenged by observations of rainbows. A letter from Benjamin Langwith, Rector of Petworth, in the Royal Society’s Philosophical Transactions of 1723, describes supernumerary rainbows – the fainter and still fainter repeats of the primary bow which can sometimes be seen to lie within its arc:

The first series of colours was as usual, only the purple had a far greater mixture of red in it than I had ever seen in the prismatic purple; under this was a coloured arch, in which the green was so predominant, that I could not distinguish either the yellow or the blue: still lower was an arch of purple, like the former, highly saturated with red, under which I could not distinguish any more colours.

Langwith then went on, as Raymond Lee and Alistair Fraser put it, to question the rainbow wisdom of the Royal Society’s President, Isaac Newton: ‘I begin now to imagine, that the Rainbow seldom appears very lively without something of this Nature, and that the suppos’d exact Agreement between the Colours of the Rainbow and those of the Prism, is the reason that it has been so little observed.’ What he accurately observed did indeed require an explanation. It came only much later, in the 19th century, when wave theory suggested that the incident and reflected rays within a water drop set up interference patterns.

It is not surprising that the Greeks, who had mastered so much of geometry, should have had some insight into the basic structure of the rainbow – Aristotle described it as a reflection which took its arcuate shape from the curved surface of an upturned hemispherical bowl of cloud. Almost every subsequent advance in our understanding of the physics of light and the physiology of sight has made it possible to say something new about the rainbow. Even now, there are no photographs of the ‘tertiary’ rainbow, which appears behind you as you look at the primary bow, although there are good accounts of it having been seen in the wild.

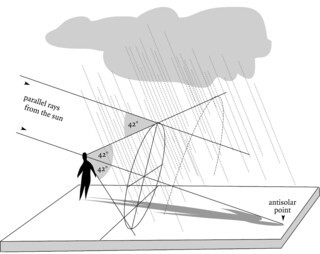
The basic architecture of the rainbow can be best thought about by imagining yourself standing looking straight at one. The sun is directly behind you, so your shadow is cast on the ground in front of you. A rainbow will appear only if the air is filled with water drops: it will be directly ahead of you, centred on the line of your shadow. If you are moving – for example, driving along a road with the sun on one side and the rainbow on the other – the rainbow travels with you. It’s a private phenomenon: two people standing side by side each see their own rainbow, not the same one from different angles – it is an image of the sun, not an object. If you measure the angle between the line from the top of the inner, primary bow to your eye and the line from your eye to the shadow of your head (known as the anti-solar point) you will find that it is about 42°. The lower the sun, the higher the bow.

The arc of the rainbow is part of a circle. The surface described by a line from your eye that sweeps the whole arc of the bow is a cone centred on the line from your eye to the anti-solar point. As the angle between that line and the line to the top of the bow is about 42°, any line from your eye along the surface of the cone – i.e. any line from your eye that intersects the bright edge of the rainbow – is also at 42°. The water drops in the rain shower which deflect sunlight so that it enters your eye to create the rainbow image are those cut by that surface – the others waste their brilliance unless another observer’s cone of view intersects them. The angle to the secondary, outer, paler bow is 51°. The colours of the inner, primary bow run through the visible spectrum from an outer red to an inner violet. Those of the outer, secondary bow are reversed. The area within the primary bow is a little brighter than the surrounding sky.

These are familiar facts about rainbows; or, rather, easily observed ones. I am probably not alone in having been unfamiliar with several of them. There are also rare phenomena to take account of, like cloud bows, which are the very pale rainbows you might see from the window of a plane, and things which are hard to see, like supernumerary rainbows. Should you be lucky enough to be somewhere where it is possible to see the never-photographed tertiary bow you would have to look back over your shoulder towards the sun, or turn round to face it. Accounts of all such phenomena must be carefully cross-examined. An explanation can make sense of what you see; it can also make you see things differently. Langwith’s ability not to see the Newtonian spectrum was itself remarkable.

The long history of the scientific rainbow runs parallel with that of the poetic one, a source of un- or even anti-scientific wonder which finds expression in myths, stories and superstitions. In The Rainbow Bridge, Lee and Fraser give the rainbows of science, art and mythology equal attention. Sometimes they illuminate one another. Goethe’s anti-Newtonian attitude (‘no aristocratic presumption has ever looked down on those who were not of its order, with such intolerable arrogance as that betrayed by the Newtonian school’) went along with a curiosity about the natural world and an interest in phenomena that Newton’s theories gave no direct account of – like colour after-images and the colour of shadows. Such things were of as much interest to painters as scientists. Turner’s Light and Colour (Goethe’s Theory) – the Morning after the Deluge – Moses Writing the Book of Genesis (1843) is an example of a poetic response to a natural wonder which acknowledges (rather obscurely) the usefulness of analysis. More often – in words or any other medium – poetry squeezes emotion from confusion and ambiguity rather than elucidating them. An awe too deep for words will not be comforted by geometry – often it seems that science’s wondering how, and art’s wondering at, are antagonistic. Keats complains that ‘Philosophy will clip an angel’s wings,’ that it will ‘Conquer all mysteries by rule and line’ and ‘Unweave a rainbow’.

Painters have not observed rainbows with Langwith’s precise and disinterested attention. Even Constable, whose meteorology was sound and scientific, dramatised the view of Salisbury Cathedral by the addition of an impossible rainbow (shadows show the sun could not be in the implied position), and Turner, despite making constant jottings from nature, was cavalier in the use he made of rainbows. Even Frederic Edwin Church, an ardent advocate of accurate accounts of nature, who is represented here by Rainy Season in the Tropics and Niagara, sometimes slipped: he achieved correctness in the latter but the drama of spurious shadows has crept into the former. Ever since nature ceased to be the court of last resort rainbows have more often appeared as symbols of a presumed mystical force than as elements in pictures which try to capture sublime moments objectively. Millet’s Spring (one of the famous rainbow pictures not referred to here), which truly captures the look of lurid storm light and of a rainbow against dark cloud, but in the domesticated landscape of an orchard, is at the end of the road. Soon Impressionism’s bright light and vivid sunsets would blind a whole generation to the softer poetry of the rainbow. The modern graphic rainbow is more often a crude symbol than a record of what is seen. Advertisers and brand-makers have picked up echoes from mythology to suggest that over, or at the end of, or under or even through their particular rainbow arch a dream can be bought for cash down.

If the rainbow is something you assumed you understood, humility follows on the unsurprising discovery that things which gave Aristotle – let alone Descartes and Newton – serious problems are lying about in your own head, like unopened mail waiting to be dealt with. Starting from scratch most of us would be hard-pressed to meet medieval science on its own ground, let alone that of the 17th century. Avicenna, who by the 11th century had seen that it was drops of water, not reflections from Aristotle’s continuous cloud that explain the rainbow, was nevertheless so far from believing that his ideas were coherent that he wrote: ‘I hesitate to put them down in this book.’ Alhazen, his contemporary, gave over an entire book of his Optics to refraction, but did not make the leap to refraction within water drops as a cause of the rainbow. Medieval scholars made advances, but were often dragged off the right path by clinging too firmly to Aristotle’s coat tails. Albertus Magnus rightly says that both refraction and reflection are involved; Roger Bacon measures the 42° angular dimension of the rainbow; Theodoric of Freiberg has two refractions and a reflection within a raindrop, but places the drops on the surface of a meteorological sphere. Kepler arrived at refraction as the source of the rainbow’s colours – but muffed the calculation of which rays (those most or those least refracted) were responsible for the visible phenomenon.

Descartes arrived at a law of refraction which properly relates the angles of the incident and refracted rays, and who saw clearly that the light from the rainbow comes not from a surface but from any illuminated drop at the right position in relation to the observer’s eye within the whole volume of the rain shower. Although he gave a correct account of the way parallel rays of sunlight, striking the curve of the raindrop at different angles, are differently refracted, so that those which are refracted least cluster more closely than those which are refracted most, he was confused about the way different colours are differently refracted.

It was Newton who saw that constituent colours of rays of white light entering the drop are variably refracted. The 42° cone from the eye describes the position of raindrops which project the red part of the spectrum. At a slightly smaller angle the eye receives light from the blue end.

The simplest, abstract rainbow of perfectly round drops of water and full-spectrum white light cannot explain every shimmer and break in real rainbows, which may be subject to, for example, filtered sunlight, larger or smaller raindrops and drops flattened by their fall through the air. In 1838, George Biddell Airy published a ‘complete theory’ of the rainbow but, despite giving a good mathematical description of the effect of those variables – drop size and so on – still left room for refinement. Lee and Fraser write that ‘while it is still useful for analysing the features of natural rainbows, it is unsuitable for explaining precisely the myriad details of artificial rainbows.’

The mathematical detail of those explanations – like the detail of Airy’s (not to mention Newton’s, Descartes’s and Maxwell’s) – are beyond the scope of The Rainbow Bridge. Lee and Fraser take you to a border only to be crossed with proper mathematical equipment; that you wish you had it is one sign of the success of their enterprise. By showing how apparently well-buttoned-up rainbow theories came undone they make old science seem as difficult as it was. They compare scientific progress to removing layers from an onion – there is always another to be peeled back. But it is progress: the new models are more complete and coherent. On the other hand, the symbolic rainbow images Lee and Fraser show – from the rainbow Christ sits on in Memling’s Last Judgment and the one Elizabeth I holds in Isaac Oliver’s Rainbow Portrait to those in the sign outside the Rainbow Motel or round a tunnel entrance north of San Francisco (more than one culture has believed that if you go through the rainbow arch your sex changes) – suggest that the rainbow as symbol has exhausted most of its power. Unlike the scientific one, it is not constantly renewed by the need for fresh, ever more detailed explanations.