James Clerk Maxwell, a Scotsman who lived from 1831 to 1879, was a scientist of outstanding stature. Bearing his name, apart from the famous ‘demon’, is the set of fundamental equations that he discovered, governing the behaviour of electricity, magnetism and light. He also found, among many other things, the basic equation for the distribution of velocities of the molecules in a gas in equilibrium, and made other profound contributions to the statistical study of the molecules in a gas, relating to the Second Law of thermodynamics – which is what Maxwell’s ‘demon’ was all about. Earlier, he had worked out the dynamics of Saturn’s rings (mainly in 1856, showing, in particular, that the rings as a whole could not be solid annular objects, but must be composed of very large numbers of tiny bodies): work which found dramatic confirmation recently in the pictures sent back from the Voyager space-probes. In addition to his important contributions to the study of physical fields and of fluid systems composed of myriads of particles, he contributed to the study of colour vision and colour blindness, and produced (in 1861) the first ever photograph in full colour. He is now generally accepted as the greatest theoretical physicist of the period between Newton and Einstein, even if, to the public at large, Maxwell’s name seems to be almost unknown. Perhaps it says something about our cultural values that, in informed society, people may never have heard of a scientist such as Maxwell when even a British schoolboy would be considered grossly uneducated if he had never heard of Dickens.
The publication of the first volume (of three) of Maxwell’s scientific papers and letters gives us a rare opportunity to acquaint ourselves with some of the thought processes of this extraordinary man in his formative years. He was almost unbelievably precocious. Before he was fifteen, he had written a paper that was subsequently presented to the Royal Society of Edinburgh, and three years later published a paper on the equilibrium of elastic solids in the Society’s Transactions. Yet one gets the impression that Maxwell himself, though he was evidently aware that his own abilities and insights were more penetrating than those of most of his fellows, would have been surprised to find that his status in the world of physicists was later to reach such a pinnacle. His slightly older contemporary William Thompson (later Lord Kelvin) was even more precocious than Maxwell, matriculating at the University of Glasgow at the astonishing age of ten and becoming a professor there at a mere 22. Thompson’s scientific standing among his contemporaries appears to have been considerably in excess of Maxwell’s. Maxwell’s letters to him in this volume reveal not only his great respect for Thompson but also his own very considerable modesty in respect of his abilities and achievements. Thus, nine years after discovering his epoch-making electrodynamic equations, he referred to them, in his Presidential address to the British Association of 1870, merely tangentially, as ‘another theory of electricity which I prefer’.
This first volume of Maxwell’s papers provides a fascinating, if at times frustrating experience. That it should be frustrating is inevitable, since it is a collection of Maxwell’s papers and letters alone, and one can only infer what the reactions of his correspondents must have been. Towards the end of the volume, Maxwell discusses the implications of his embryonic electrodynamic theory. He writes excitedly to Michael Faraday about his discovery that, according to his own theory, electric and magnetic fields would propagate with a speed that appeared to be identical with the speed of light – from which he concludes, as he states in a subsequent letter to Thompson, ‘that I think I have reason to believe that the magnetic and luminiferous media are identical’ – i.e. that the mysterious and elusive nature of light can now finally be understood as an electromagnetic effect. These ideas confirmed Faraday’s deep intuition about the nature of light, which had been stimulated by his fundamental experiments, and it is frustrating not to be able to read his reaction to Maxwell’s letter. Similarly, it would have been fascinating to know how Thompson reacted: it is said that, to the end of his life, he never found himself able to embrace Maxwell’s equations fully, though he outlived Maxwell by nearly thirty years.
The breadth of Maxwell’s interests, like the depth and care with which he pursued them, is astounding. He reveals himself to be an applied mathematician of consummate skill, a geometer of natural ability and great inventiveness, an acute researcher into biological matters as they relate to the perception of colour and other matters (such as polarised light), an ingenious inventor of practical devices, and an innovative and careful experimenter. And all this in addition to being the theoretical physicist whose insights underlie so much of the physics of our own century.
It is striking how his abilities in one area helped him to make advances in another. As Maxwell himself said, there were ‘no water-tight compartments’ in his mind. He often thought in mechanical terms, even when contemplating abstract physical ideas. It is now accepted that one of his most fundamental achievements (building on Faraday’s earlier experimental findings) was to break away from the ‘Newtonian’ picture, according to which the world consisted of discrete particles acting on one another by forces. It was by introducing the concept of continuously varying ‘fields’ – electric and magnetic – as a separate part of physical reality that he was able to do this, though he seems to have been led to these new ideas by thinking in terms of mechanical models involving wheels and smaller idle wheels. Such models helped him to find the consistent viewpoint that led him to his electrodynamical equations, though later he was able to dispense with such crutches and allow his equations to provide all the ‘substance’ required by his concept of an electromagnetic field.
This volume contains other striking instances of Maxwell’s mechanical way of thinking about abstract ideas. He showed how to construct a mechanical model demonstrating the complicated motions of the individual particles that make up Saturn’s rings, which he had deduced by means of sophisticated equations. The model was actually constructed (by Charles Ramage, of the Aberdeen instrument-makers Smith and Ramage) in 1858. Maxwell also constructed numerous optical devices, in connection, in particular, with his researches into colour vision. The frontispiece to the volume shows him in the autumn of 1855 holding his colour top, a picture which conveys something of the lighthearted and humorous, if somewhat detached attitude to life also revealed by Maxwell’s many letters to his friends – at least in the earlier stages of his life.
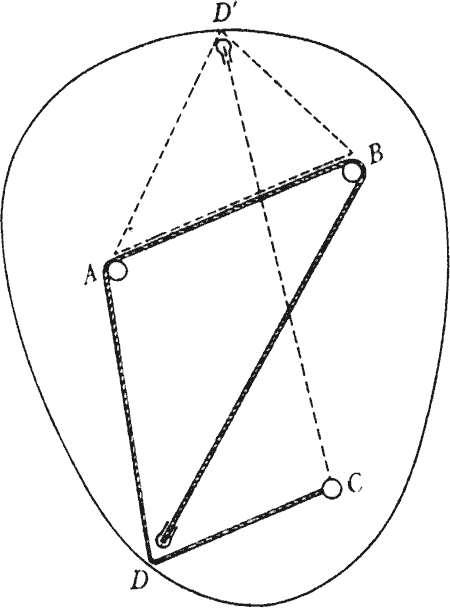
The connections between Maxwell’s mechanical interests and his mathematical ones were evident even in his earliest paper, which he wrote in 1846, as a mere schoolboy of 14. It was on the geometry of Cartesian ovals, though Maxwell was originally unaware of Descartes’s work in this area. The young Maxwell devised ingenious ways of describing such curves with string, pins, paper and pencil. To gain a flavour of what it involved, try to imagine a device for drawing a curve in a plane, the curve being defined as the locus of points for which the sum of its distances from three fixed points in the plane is a constant. Maxwell’s ingenious solution is illustrated in the figure on this page. Three pins are placed at the three points and a string is looped round two of them and fixed at the third, the pencil is attached to the other end of the string, and the string loops round the pencil. Maxwell gave numerous other examples, many of them much more complicated than this one. He also proved a number of theorems about these curves, and developed their theory in considerable detail. This work led on to other geometric studies, involving curves rolling on one another and the like.
His early advancement as a scientist owed much to his close relationship with his father, his mother having died when he was nine years old (of the same stomach cancer that would later claim him at the same youthful age of 48). Despite his many early successes, and the recognition he undoubtedly received (though it was in no way comparable to his ultimate scientific status), his career was not without its problems. He had been appointed to the Professorship of Natural Philosophy at Marischal College in Aberdeen in 1856, but early in 1860, it was proposed that the two colleges in Aberdeen (the other being Kings College) were to be ‘fused’ to become the University of Aberdeen. This meant that, in each separate subject, only one of the two professors would be retained. Generally it was the younger of the two who kept his professorship, but in Maxwell’s case the Commissioners made an exception, and Maxwell found himself without a job. (It is perhaps reassuring that the treatment of universities in our own time may not, after all, involve more folly than it did in the mid-19th century!) Maxwell applied for the Professorship of Natural Philosophy at Edinburgh, but was passed over, his old school-fellow P. G. Tait being appointed instead. However, in July 1860 he was successful in obtaining the professorship at King’s College, London, which is where he did his fundamental work on electromagnetism.
His inaugural lectures at both Marischal and King’s College London are reproduced here. Together with some of his other lectures and letters, they reveal a profound interest in a number of philosophical issues: the relation between mathematics and physics, and the relation between physics and morality and other matters of the mind. James Clerk Maxwell was a natural philosopher in the deepest sense, and this volume gives us the opportunity to study him directly and to learn from one of the intellectual giants among scientists.
Send Letters To:
The Editor
London Review of Books,
28 Little Russell Street
London, WC1A 2HN
letters@lrb.co.uk
Please include name, address, and a telephone number.